函数的间断点有（     ）。  A: 1个 B:2个 C:3个 D: 4个 答案: 3个

1. 创立了微积分的数学家是 (      ).   

A:牛顿
B:柯西
C:拉格朗日
D:莱布尼兹
E:笛卡尔
答案: 牛顿;莱布尼兹

设函数

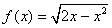
的定义域为 (      ).A

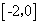
B

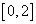
C

D

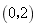
A:A
B:B
C:C
D:D
答案: B

下列各对函数中，两函数相同的是（   ）A

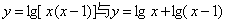
B

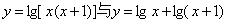
C

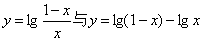
D

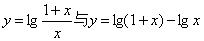
A:A
B:B
C:C
D:D
答案: C

函数 

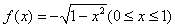
的反函数 

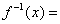
（    ） A

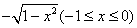
B

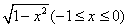
C

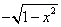
D

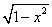
A:A
B:B
C:C
D:D
答案: B

下列关系中，是复合函数关系的是（    ）.A

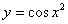
B

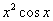
C

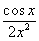
D

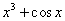
A:A
B:B
C:C
D:D
答案: A

函数 

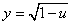
与

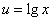
能构成复合函数 

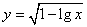
的区间为（   ） .A

B

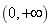
C

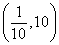
D

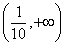
A:A
B:B
C:C
D:D
答案: A

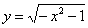
  是函数关系式.（   ）.

A:对
B:错
答案: 错

函数 

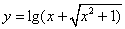
是奇函数.（   ）.

A:对
B:错
答案: 对

函数 

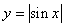
是周期函数，周期为

.（   ）

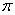
A:对
B:错
答案: 对

任何两个函数都能构成复合函数.（   ）

A:对
B:错
答案: 错

分段函数一定不是初等函数

A:对
B:错
答案: 错

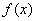
在点 

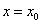
处有左极限”是当 

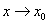
时 

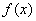
有极限的（     ）

A:必要条件    
B:充分条件
C:充要条件
D:无关条件
答案: 必要条件    

已知当

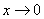
时，

是无穷大量，下列变量当

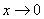
时一定是无穷小量的是（     ）A

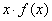
B

C

D

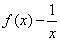
A:A
B:B
C:C
D:D
答案: C

函数极限

（    ）.

A:2
B:1
C:0
D:不存在
答案: 0

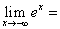
（     ）A.0
B.1C.2D

A:A
B:B
C:C
D:D
答案: A

设函数

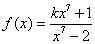
，且

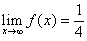
，则

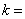
（     ）A

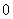
B

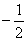
C

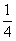
D

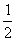
A:A
B:B
C:C
D:D
答案: C

极限

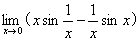
的结果是（    ）

A:-1
B:1
C:0
D:不存在
答案: -1

数列极限 

 (      ).A

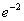
B

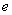
C

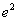
D

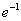
A:A
B:B
C:C
D:D
答案: A

 下列结论正确的是（    ）A

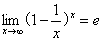
B

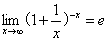
C

D

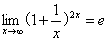
A:A
B:B
C:C
D:D
答案: C

 当

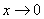
时，

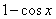
与2

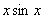
相比较是（      ）

A:低阶无穷小量
B:同阶无穷小量
C:等价无穷小量
D:高阶无穷小量
答案: 同阶无穷小量

函数极限

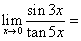
 (      ).A

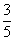
B

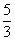
C

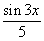
D.0

A:A
B:B
C:C
D:D
答案: A

设函数

连续，则

（     ）

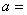
A:0
B:1
C:2
D:3
答案: 3

 设函数

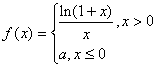
连续，则

（     ）

A:0
B:1
C:2
D:3
答案: 1

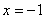
是函数 

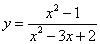
的（     ）

A:连续点
B:可去间断点
C:跳跃间断点
D:第二类间断点
答案: 连续点

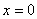
是函数 

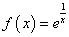
的（     ）

A:连续点
B:可去间断点
C:跳跃间断点
D:第二类间断点
答案: 第二类间断点

分段函数必有间断点（      ）

A:对
B:错
答案: 错

 当时，是的（      ）。

A: 低阶无穷小量
B: 同阶无穷小量
C: 等价无穷小量
D: 高阶无穷小量
答案:  等价无穷小量

（      ）。 

A: -2
B:-3 
C: 3
D: 2
答案:  2

（      ）。 

A: 1
B: 
C: 
D: 
答案:  

当时，下列说法正确的是（      ）。 

A: 是无穷小量
B: 是无穷小量
C: 是无穷大量
D:是无穷大量
答案:  是无穷小量

（      ）。 

A: -2
B: -3
C: 3
D: 2
答案:  -3

（      ）。 

A: 
B: -3
C: 3
D: 0
答案:  0

 函数在点处的左右极限都存在，则在处的极限也存在。（     ）

A:对
B:错
答案: 错

函数极限 (      )。 

A: 
B: 
C: 
D: 0
答案:  

 设函数，则（     ）。

A: 0
B: 1
C: -1
D: 不存在
答案:  不存在

下列极限正确的是（     ）。 

A: 
B: 
C: 
D: 
答案:  

“在点处左右极限存在并且相等”是当时有极限的（     ）。 

A: 必要条件
B: 充分条件
C: 充要条件
D: 无关条件
答案:  充要条件

极限的结果是（    ）。 

A: -1
B: 1
C: 0
D: 不存在
答案:  1

下列变量在给定的变化过程中，不是无穷大量的是（    ）。 

A: 
B: 
C: 
D: 
答案:  

设函数，且，则（     ）。 

A: 0
B: 
C: 
D: 
答案:  

（     ）。 

A: 0
B: 1
C: 2
D: 
答案:  0

函数的间断点有（     ）。 

A: 1个
B:2个
C:3个
D: 4个
答案: 3个

x=2是函数的（     ）。

A: 连续点
B: 可去间断点
C: 跳跃间断点
D: 第二类间断点
答案:  第二类间断点

设函数连续，则（     ）。 

A: 0
B: 1
C: 2
D: 3
答案:  2

是函数

的（     ）。 

A: 连续点
B: 可去间断点 
C: 跳跃间断点
D: 第二类间断点
答案:  可去间断点 

若要修补，使其在点处连续，则要补充定义（   ）。 

A: 
B: 3
C: 1
D: 
答案:  

设函数在点处可导，且，则等于(      )。

A: 
B: 
C: 2
D: -2
答案:  

下列函数（    ）中在处可导。 

A: 
B: 
C: 
D: 
答案:  

 在曲线与直线的交点处，的切线方程为（   ）。

A: 
B: 
C: 
D: 
答案:  

 函数在连续是在点可导的（   ）条件。

A: 充分
B: 必要
C: 充要
D: 无关
答案:  必要

已知则（   ）。 

A: 
B: 
C: 
D: 
答案:  

已知则（   ）。 

A: 
B: 
C: 
D: 
答案:  

已知则（    ）。 

A: 
B: 
C: 
D: 
答案:  

函数 ,可导，则 （    ）。 

A: 
B: 
C: 
D: 
答案:  

函数 ，则 （    ）。 

A: -35
B: -27
C: -19
D: -7
答案:  -7

函数 ,具有二阶连续导数，则 （    ）。 

A: 
B: 
C: 
D: 
答案:  

函数 ,具有二阶连续导数，则 （    ）。 

A: 
B: 
C: 
D: 
答案:  

设 ，则（    ）。 

A: 
B: 
C: 
D: 
答案:  

设 ，则（    ）。 

A: 
B: 
C: 
D: 
答案:  

已知函数由方程所确定,则 （      ）。

A: 
B: 
C: 
D: 
答案:  

已知函数由方程所确定,则（    ）。 

A: 2
B: 1
C: 0
D: 3
答案:  1

，则（      ）。 

A: 
B: 
C: 
D: 
答案:  

若函数可在点处可微，且，则当，必有 （   ）。 

A: 
B: 
C: 
D: 
答案:  

，则（      ）。 

A: 
B: 
C: 
D: 
答案:  

若函数在点处可微，是在点处连续的（    ）。 

A: 充分且必要条件   
B: 必要非充分条件
C: 充分非必要条件
D: 既非充分也非必要条件
答案:  充分非必要条件

设 ，则（     ）。 

A: 
B: 
C: 
D: 
答案: