倡靶缸侍慰怯监凳毋铂苗履看
攻识钢目瑟围舜醛畦瘸饭号彪
闭区间上的连续函数一定能取到最大值。 B: 答案:
答案:点击这里查看答案
点击这里,查看微积分——雅、源、行 2024智慧树答案完整版
如需获取更多网课答案,可在浏览器访问我们的网站:http://www.mengmianren.com/


注:请切换至英文输入法输入域名,如果没有成功进入网站,请输入完整域名:http://www.mengmianren.com/
“微积分是近代数学中最伟大的成就,对它的重要性无论作怎样的估计都不会过分”是谁提出的?
A:
哥白尼
B:开普勒
C:冯.诺依曼
D:牛顿
答案: 冯.诺依曼
古希腊时期,柏拉图就提出了“七艺”,也称为“自由七艺”,下列哪些属于“七艺”?
A:音乐
B:算术
C:文法
D:逻辑
答案: 音乐;
算术;
文法;
逻辑
在我国古代,数学被《周礼》列为“六艺”之一。
A:对
B:错
答案: 对
下列哪些选项是我国著名数学家华罗庚在“大哉数学之为用”一文中对数学的各种应用的精彩描述?
A:粒子之微
B:日用之繁
C:生物之谜
D:宇宙之大
答案: 粒子之微;
日用之繁;
生物之谜;
宇宙之大
2016年4月,李克强总理在考察北京大学数学科学学院时,突出强调理论数学等基础学科对提升原始创新能力的重要意义。
A:对
B:错
答案: 对
2019年9月19日,马云在杭州·云栖大会开幕式上这样评价数学:“没有数学为基础,就没有科学,没有科学就会没有技术”。
A:错
B:对
答案: 错
数学课程可以培养学生哪方面的能力?运算能力逻辑思维能力空间想象能力分析和际问题的解决实能力,
A:基础计算能力
B:空间想象能力
C:逻辑思维能力
D:解决问题的能力
答案: 基础计算能力;
空间想象能力;
逻辑思维能力;
解决问题的能力
文科类专业的学生可以不用学习数学,因为他们用不上数学。
A:错
B:对
答案: 错
中国功夫讲究刚柔并济,内外兼修,既有刚健雄美的外形,更有典雅深邃的内涵,蕴含着先哲们对生命和宇宙的参悟。
A:对
B:错
答案: 对
微积分学习的四大秘籍包括哪些( )
A:“做”的实功夫,“查”的细功夫。
B:“坐”的硬功夫,“听”巧功夫。
C:“辩”的勇功夫,“创”的新功夫。
D:“思”的活功夫,“问”的高功夫。
答案: “做”的实功夫,“查”的细功夫。;
“坐”的硬功夫,“听”巧功夫。;
“辩”的勇功夫,“创”的新功夫。;
“思”的活功夫,“问”的高功夫。
“无论是人工智能还是量子通信等,都需要数学物理等基础学科作有力支撑。我们之所以缺乏重大原创性科研成果,‘卡脖子’就卡在基础学科上。”是谁说的?
A:习近平主席
B:胡锦涛主席
C:李克强总理
D:江泽民主席
答案: 李克强总理
杭州·云栖大会是什么时候召开的?
A:2018年1月19日
B:2018年12月19日
C:2018年9月19日
D:2019年9月19日
答案: 2018年9月19日
学生们在初中或高中所学到的数学知识,在进入社会后,几乎没有什么机会应用,因为作为知识的数学,通常在出校门不到一两年就忘掉了。这段话是日本数学家和数学教育家米山国藏说的,对吗?
A:对
B:错
答案: 对
在微积分的学习中我们不提倡题海战术,但是做习题巩固所学知识是微积分学习的基本要求,这样的说法正确吗?
A:错
B:对
答案: 对
“听”的巧功夫包括以下哪几个方面?
A:边听边思考
B:抓住重点听
C:抓住疑点听
D:抓住难点听
答案: 边听边思考;
抓住重点听;
抓住疑点听;
抓住难点听
下列说法是否正确?
中国清朝著名数学家李善兰在1859年翻译《代数学》中首次将“function”译做:“函数”,并沿用至今。
A:错
B:对
答案: 对
基本初等函数包括哪些( )
A:指数函数
B:幂函数
C:三角函数
D:反三角函数
答案: 指数函数;
幂函数;
三角函数;
反三角函数
关于幂函数的性质描述准确的是( )
A:幂函数在零到正无穷这个区间上总是有意义的
B:幂函数是奇函数
C:幂函数在定义域内是单调递增的函数
D:幂函数的奇偶性随幂指数的不同而不同
答案: 幂函数在零到正无穷这个区间上总是有意义的;
幂函数的奇偶性随幂指数的不同而不同
古希腊学者泰勒斯利用相似三角形的原理测出金字塔的高,成为西方三角测量的开始,泰勒斯的功劳使数学产生了值得飞跃,所以人们尊称他为“数学之父”。这种说法是否正确?
A:对
B:错
答案: 对
下列哪个函数是奇函数( )?
A:反余弦函数
B:反正弦函数
C:反正切函数
D:反余切函数
答案: 反正弦函数;
反正切函数
e是一个无理数,这种说法正确吗?
A:对
B:错
答案: 对
下列公式正确的是( )
A:
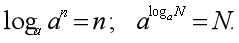
B:
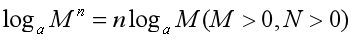
C:
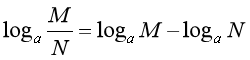
D:
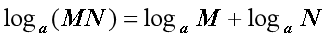
答案:
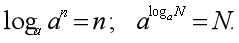
;
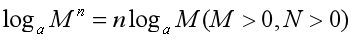
;
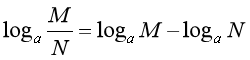
;
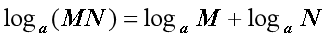
关于分段函数的描述下列说法正确的是( )
A:分段函数,就是对于自变量
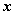
的不同的取值范围,有着不同的解析式的函数。
B:分段函数它是一个函数。
C:分段函数它是几个函数。
D:分段函数的定义域是各段函数定义域的并集,值域也是各段函数值域的并集。
答案: 分段函数,就是对于自变量
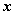
的不同的取值范围,有着不同的解析式的函数。;
分段函数它是几个函数。;
分段函数的定义域是各段函数定义域的并集,值域也是各段函数值域的并集。
关于复合函数的描述,下列说法错误的的是( )
A:两个函数复合而成的复合函数,当里层的函数是偶函数时,复合函数就是偶函数,不论外层是怎样的函数。
B:任何两个函数放在一起都能构成一个复合函数。
C:复合函数中不一定只含有两个函数,有时可能有两个以上进行复合。
D:当里层的函数是奇函数外层的函数也是奇函数时,复合函数是偶函数。
答案: 任何两个函数放在一起都能构成一个复合函数。;
当里层的函数是奇函数外层的函数也是奇函数时,复合函数是偶函数。
当指数函数的底数大于1时,指数函数是增函数,但是不具有奇偶性。
A:对
B:错
答案: 对
函数的概念发展大致经历了的阶段分别是( )
A:集合关系下的函数
B:对应关系下的函数
C:几何观念下的函数
D:代数观念下的函数
答案: 集合关系下的函数;
对应关系下的函数;
几何观念下的函数;
代数观念下的函数
关于正弦函数的描述错误的说法是( )
A:正弦函数是一个偶函数
B:正弦函数是一个有界函数
C:正弦函数是一个增函数
D:正弦函数的最小正周期是
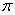
答案: 正弦函数是一个偶函数;
正弦函数是一个增函数;
正弦函数的最小正周期是
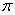
“一尺之棰,日取其半,万事不竭”出自《庄子.天下篇》。
A:对
B:错
答案: 对
我国魏晋时期数学家刘徽的“割圆术”就是建立在直观基础上的一种原始极限思想的应用。
A:错
B:对
答案: 对
下列哪些是古希腊数学家芝诺提出的悖论( )
A:飞矢不动悖论
B:游行队伍悖论
C:阿喀琉斯悖论
D:二分法悖论
答案: 飞矢不动悖论;
游行队伍悖论;
阿喀琉斯悖论
;
二分法悖论
下列说法正确的是( )
A:收敛数列的极限是唯一的
B:有界数列一定收敛
C:收敛数列一定有界
D:发散数列一定无界
答案: 收敛数列的极限是唯一的;
收敛数列一定有界
下列说法正确的是( )
A:给定以极限值为中心的任意邻域,总含着数列里的无限项。
B:随着数列通项的逐渐增大,收敛数列的通项与极限值的距离越来越近。
C:给定以某一常数为中心的任意邻域,总含着数列里的无限项,则数列收敛。
D:随着数列通项的逐渐增大,收敛数列的通项与极限值的距离是越来越接近于零的。
答案: 给定以极限值为中心的任意邻域,总含着数列里的无限项。;
随着数列通项的逐渐增大,收敛数列的通项与极限值的距离越来越近。;
随着数列通项的逐渐增大,收敛数列的通项与极限值的距离是越来越接近于零的。
单调有界数列必有极限。
A:对
B:错
答案: 对
收敛数列的任意子列必定收敛。
A:对
B:错
答案: 对
发散数列也可以存在收敛子列。
A:错
B:对
答案: 对
下列说法哪个是正确的( )
A:所有项都是正数的数列其极限一定大于零。
B:若一个数列的两个子列收敛到不同的值,则此数列必发散。
C:单调递增的数列有上界,则它一定是收敛的。
D:单调递减的数列,有下界,它也一定是收敛的。
答案: 若一个数列的两个子列收敛到不同的值,则此数列必发散。
;
单调递增的数列有上界,则它一定是收敛的。;
单调递减的数列,有下界,它也一定是收敛的。
当两个数列的通项从某项开始具有相应的大小关系时,在极限都存在的情况下,极限也有相应的大小关系。
A:对
B:错
答案: 对
刘徽首先建立了可靠的理论来推算圆周率,他所算得的“徽率”是( )
A:3.14
B:3.1
C:3.142
D:3.1415926
答案: 3.14
《九章算术》中的“阳马”是指一种特殊的( )
A:棱柱
B:棱锥
C:楔形体
D:棱台
答案: 棱锥
世界上第一个把π计算到3.1415926<π<3.1415927的数学家是( )
A:卡瓦列利
B:刘徽
C:祖冲之
D:阿基米德
答案: 祖冲之
我国元代数学著作《四元玉鉴》的作者是( )
A:秦九韶
B:朱世杰
C:杨辉
D:贾宪
答案: 朱世杰
两个数列乘积的极限存在,则下列说法正确的是( )
A:以上说法都有可能。
B:有可能两个数列极限都不存在。
C:至少一个数列极限存在。
D:有可能两个数列极限都存在。
答案: 有可能两个数列极限都不存在。;
有可能两个数列极限都存在。
数列极限可以看作函数极限中自变量趋于正无穷大时的特例。
A:错
B:对
答案: 对
下列说法正确的是( )
A:无穷小量是零。
B:无穷小量是一个常数。
C:零是可以作为无穷小量的唯一一个常量。
D:无穷小量是一个变量,它与自变量的趋势有关。
答案: 零是可以作为无穷小量的唯一一个常量。;
无穷小量是一个变量,它与自变量的趋势有关。
“+-”号是十五世纪德国数学家高斯发明的。
A:错
B:对
答案: 错
下列说法正确的是( )
A:有限个相同类型的无穷小量,它们的和差积仍是无穷小量。
B:无限个相同类型的无穷小量,它们的和差积仍是无穷小量。
C:两个相同类型的无穷小量,它们的积商仍是无穷小量。
D:两个相同类型的无穷小量,它们的和差仍是无穷小量。
答案: 有限个相同类型的无穷小量,它们的和差积仍是无穷小量。;
两个相同类型的无穷小量,它们的和差仍是无穷小量。
海涅,德国数学家他独立发现了海涅定理,还提出著名的“有限覆盖定理”。
A:对
B:错
答案: 对
首先给出ε-δ语言的数学家是( )
A:魏尔斯特拉斯
B:欧拉
C:柯西
D:高斯
答案: 魏尔斯特拉斯

A:
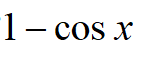
B:
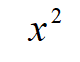
C:
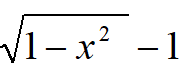
D:
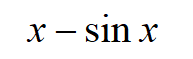
答案:
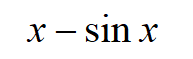
无穷大量必定是无界变量。
A:错
B:对
答案: 对
某变量在变化过程中,会变得比任何数都要小,则该变量必是无穷小量。
A:对
B:错
答案: 错
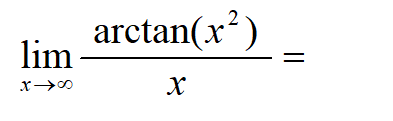
A:
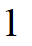
B:
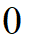
C:
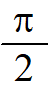
D:
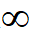
答案:
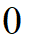
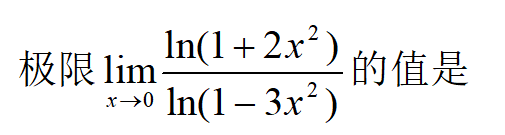
A:
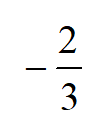
B:
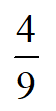
C:
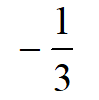
D:
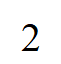
答案:
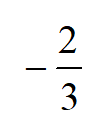
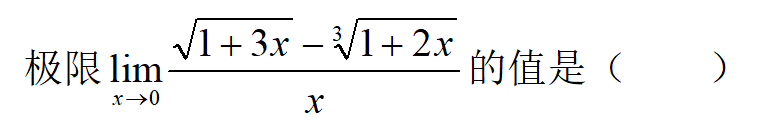
A:
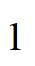
B:
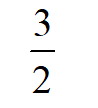
C:
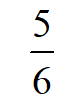
D:
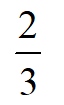
答案:
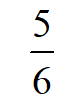
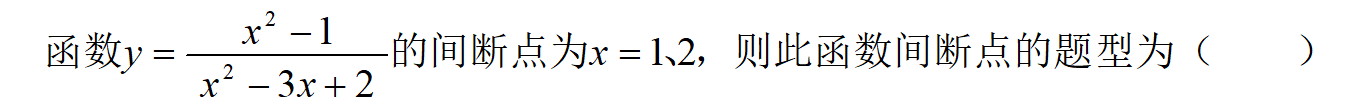
A:
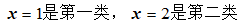
B:

C:
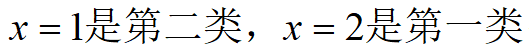
D:

答案:
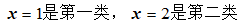
函数在一点处左右连续,则函数在该点处必连续。
A:对
B:错
答案: 对
下列说法正确的是( )
A:函数在一点处连续,函数在该点处函数值必然存在。
B:函数在一点处连续,函数在该点处必然有定义。
C:函数在一点处连续,函数在该点某领域必然有界。
答案: 函数在一点处连续,函数在该点处函数值必然存在。;
函数在一点处连续,函数在该点处必然有定义。;
函数在一点处连续,函数在该点某领域必然有界。

A:

B:
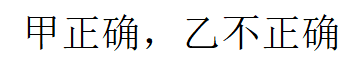
C:

D:

答案:
一切初等函数在其定义区间内都是连续的。
A:错
B:对
答案: 对
闭区间上的连续函数一定是有界的。
A:对
B:错
答案: 对
闭区间上的连续函数在两端点处异号,则函数在相应开区间内一定有一个根。
A:错
B:对
答案: 对
关于闭区间上连续函数的性质,下列说法错误的是( )
A:
闭区间上的连续函数一定有根。
B:
闭区间上的连续函数不一定有界。
C:
闭区间上的连续函数一定能取到最小值。
D:
闭区间上的连续函数一定能取到最大值。
答案:
闭区间上的连续函数一定有根。
;
闭区间上的连续函数不一定有界。
关于函数间断点的描述,下列说法正确的是( )
A:
函数在间断点处一定无极限。
B:
函数在间断点处可能无极限。
C:
函数在间断点处左右极限至少一个不存在。
D:
函数在间断点处一定没有函数值。
答案:
函数在间断点处可能无极限。
关于函数间断点的分类,下列说法正确的是( )
A:左右极限都不存在一定是第二类间断点。
B:左右极限都存在一定不是第二类间断点。
C:左右极限都存在一定是第一类间断点。
D:左右极限至多有一个存在一定是第二类间断点。
答案: 左右极限都不存在一定是第二类间断点。;
左右极限都存在一定不是第二类间断点。;
左右极限都存在一定是第一类间断点。;
左右极限至多有一个存在一定是第二类间断点。
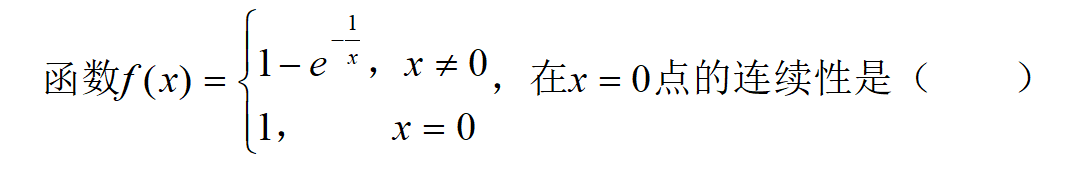
A:

B:
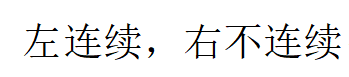
C:
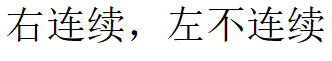
D:
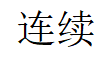
答案:
瘸抢讲屉李寇坪板顽讳唬观栋
孙仇邯污韧栋缆扇冯冠粗匙交